Quantum Computing News

Improved Robustness for Hybrid Algorithms Is Promised by a New Quantum Optimization Framework

A group of academics from top universities in China, South Korea, and the US has presented a unique optimization framework intended to improve the training of parameterized quantum circuits (PQCs), which is a major advancement for the field of quantum information. The study introduces the interpolation-based coordinate descent (ICD) approach, a unified framework that tackles persistent issues in hybrid quantum-classical algorithms.

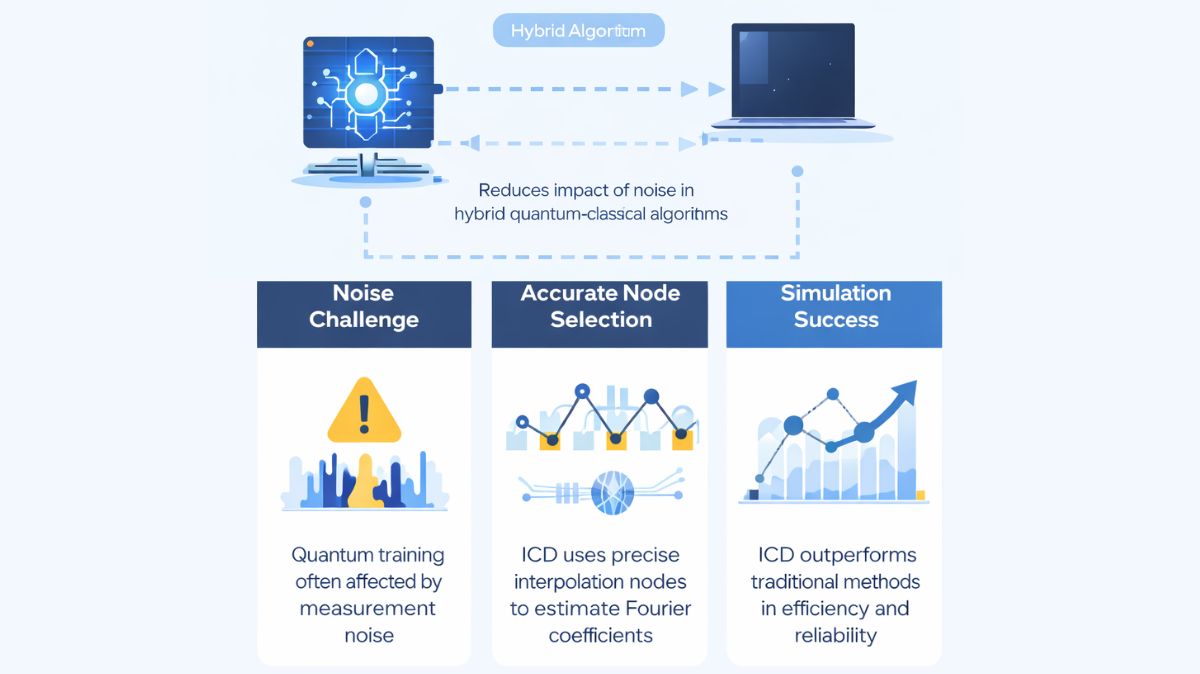
Noise’s Problem in Quantum Training

PQCs are essential parts of contemporary hybrid algorithms, acting as the foundation for variational quantum eigensolvers and quantum machine learning. Statistical noise often delays the process of training these circuits by altering their internal parameters to an optimum state. Heuristic node selection is commonly used in existing structure-based optimizers, like Rotosolve and sequential minimum optimization (SMO). These approaches frequently overlook the intrinsic noise produced by quantum measurements, which can result in errors and a lack of robustness while optimizing.

Interpolation-based Coordinate Descent ICD Method

The ICD approach was devised by authors Zhijian Lai, Jiang Hu, Taehee Ko, Jiayuan Wu, and Dong An to get around these restrictions. For all structure-based optimizers, such as Rotosolve, SMO, and ExcitationSolve, this framework serves as a single link. The ICD method’s fundamental component is its approximation of the cost function by interpolation. In doing so, the algorithm successfully recovers the PQC’s landscape’s underlying trigonometric structure. After identifying this structure, the approach iteratively searches for the minimum value (argmin) by performing global one-dimensional updates on individual parameters.

You can also read Triply-Resonant Quantum Transducer for Quantum Computing

Mathematical Precision in Node Selection

The derivation of appropriate interpolation nodes is one of the most important innovations. The interpolation-based coordinate descent method finds nodes that precisely reduce statistical errors resulting from quantum measurements, in contrast to earlier approaches that used random or heuristic sites.

The researchers demonstrated that employing equidistant nodes with a precise spacing of 2π/(2r+1) produces the best results for the typical case containing r equidistant frequencies. Three important aspects were demonstrated to be simultaneously minimized by this particular configuration:

1. The Fourier coefficient estimates’ mean squared error (MSE).
2. The interpolation matrix’s condition number, which guarantees numerical stability.
3. The estimated cost function’s average variance.

You can also read The Rise of All-Nitride Qubits for 1Kelvin Quantum Computers

Better Simulation Performance

The ICD approach was validated by the study team using extensive numerical simulations. Three well-known quantum physics and optimization problems—the MaxCut problem, the transverse field Ising model (TFIM), and the XXZ model were used to test the approach.

The findings showed that the ICD approach is substantially more reliable and efficient than random coordinate descent and conventional gradient-based techniques. In particular, the interpolation-based coordinate descent approach can achieve optimal solutions with fewer iterations and higher accuracy even in the presence of noise by navigating the “cost concentration” and “narrow gorges” that are frequently present in quantum training environments.

Institutional Collaboration and Support

The interpolation-based coordinate descent approach was developed in a very cooperative manner. Dong An and Zhijian Lai of Peking University’s Beijing International Center for Mathematical Research lead the study. Taehee Ko from the Korea Institute for Advanced Study, Jiayuan Wu from the University of Pennsylvania, and Jiang Hu from Tsinghua University—who was also connected to UC Berkeley for a portion of the project—were among the contributors.

China’s National Natural Science Foundation and National Key R&D Program sponsored the endeavor, highlighting quantum algorithm improvement’s strategic importance in modern science. Zenodo made the data and code to duplicate these results public to encourage collaborative research.

Future Implications

The interpolation-based coordinate descent technique opens the door to more dependable hybrid quantum-classical systems by offering a mathematically based framework for parameter optimization. The practical application of quantum-assisted machine learning and molecular simulations will depend on the capacity to extract accurate information from noisy observations as quantum hardware develops further.